Logo IECL Logo Inria Logo ANR Logo IAEM Logo IUF Logo Reseau EDP Logo UFR MIM

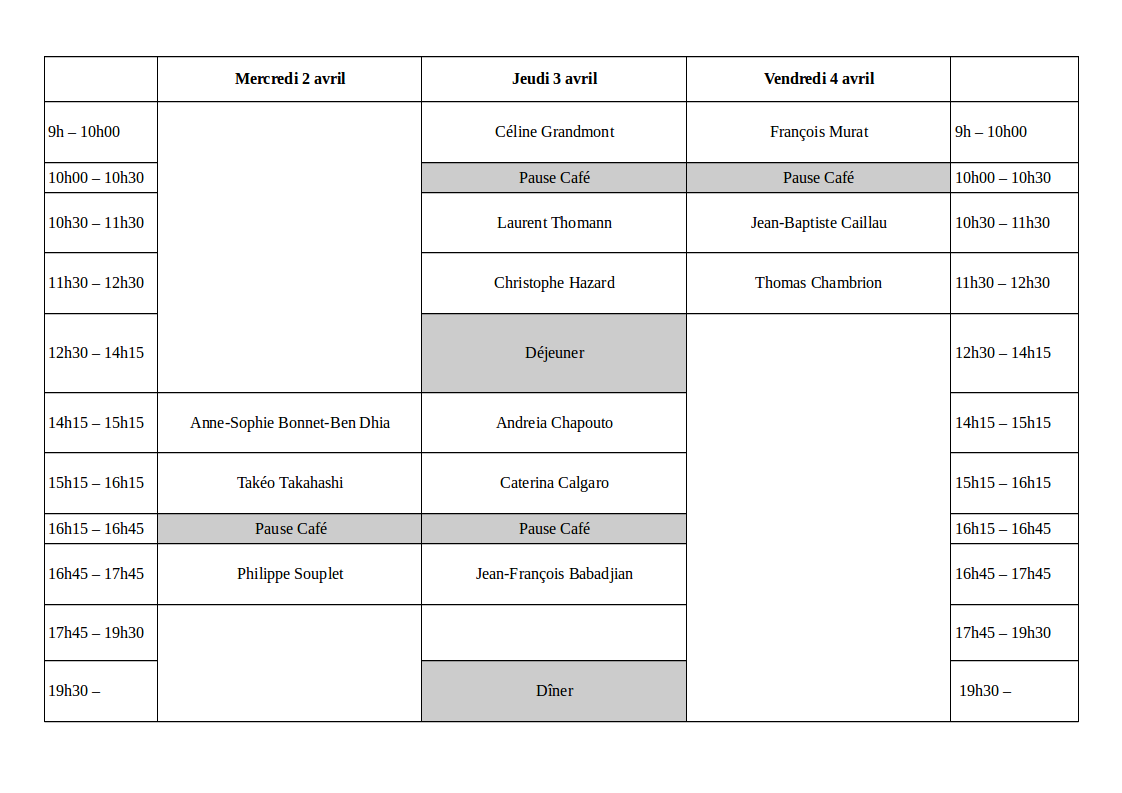
Du 2 au 4 avril 2025
Amphi Hedy Lamarr (Petit Amphi), Bâtiment de l’UFR MIM, Campus du Technopole, Metz.

 

 

Dîner

Le dîner de la conférence aura lieu le jeudi 3 avril à partir de 19h30 au restaurant El Theatris , situé au 2, rue de la comédie, 57000 Metz.

 

Conférenciers et titres des exposés

Cliquer sur le titre d’un exposé pour vous déplacer jusqu’au résumé correspondant.
 

Jean-François Babadjian (Université Paris Saclay) Plasticité parfaite : du calcul des variations aux systèmes hyperboliques
Anne-Sophie Bonnet-Ben Dhia (CNRS, Inria & Ensta, Paris) Spectre et pseudospectre de fréquences sans réflexion : l’effet zip
Jean-Baptiste Caillau (CNRS, Inria & Université Côte d’Azur, Nice) Optimisation de déterminants d’opérateurs Sturm-Liouville
Caterina Calgaro (Inria & Université de Lille) Schémas Volumes Finis pour les équations de Navier-Stokes quantique
Thomas Chambrion (Université de Bourgogne, Dijon) Contrôle de systèmes quantiques à commutations
Andreia Chapouto (CNRS & Université de Versailles Saint-Quentin) Théorie des chemins rugueux pour les équations dispersives non-linéaires stochastiques avec des bruits multiplicatifs
Céline Grandmont (Inria Paris) Analyse mathématique et numérique d’un modèle poromécanique linéarisé pour des milieux incompressibles et quasi-incompressibles. Application à la micro-circulation
Christophe Hazard (CNRS, Inria & Ensta, Paris) Peut-on confiner des ondes en milieu ouvert ?
François Murat (CNRS & Sorbonne Université) Un problème elliptique singulier unidimensionnel qui présente des résultats inattendus
Philippe Souplet (Univesité Sorbonne Paris Nord) Singularités des solutions et théorèmes de type Liouville pour l’équation de Hamilton-Jacobi diffusive
Takéo Takahashi (Inria Nancy — Grand Est) Méthode de la platitude pour la contrôlabilité d’un système d’équations de la chaleur
Laurent Thomann (Université de Lorraine) Existence et unicité pour le modèle \Phi^4_3 avec laplacien harmonique

 

 

Liste des exposés dans l’ordre chronologique

Ce travail fait l’objet d’une collaboration avec Lucas Chesnel, Christophe Hazard et Vincent Pagneux. Nous nous intéressons au calcul de fréquences dites « sans réflexion » dans un guide d’onde infini localement perturbé (il peut s’agir d’ondes acoustiques ou électromagnétiques). Une fréquence est dite sans réflexion lorsqu’il existe à cette fréquence une onde qui est transmise à travers la perturbation sans produire de réflexion. Nous avons montré dans [1] que la recherche de ces fréquences peut se formuler mathématiquement comme un problème de valeurs propres non autoadjoint pour un opérateur non borné. L’idée est d’introduire de part et d’autre de la perturbation une dilatation complexe de la variable longitudinale, avec des coefficients de dilatation différents de chaque côté de la perturbation, conjugués l’un de l’autre. Ceci rend l’onde sans réflexion exponentiellement décroissante à l’infini. On peut alors tronquer le guide et discrétiser le problème à l’aide d’éléments finis. C’est la méthode des PMLs (pour Perfectly Matched Layers) conjuguées.

Le problème spectral des fréquences sans réflexion donne lieu à des phénomènes assez surprenants. Il est suffisant pour les décrire et les expliquer de considérer un problème monodimensionnel analogue à celui du guide d’ondes. Je consacrerai donc l’essentiel de ma présentation à l’équation de Helmholtz 1D, avec une variation locale de la vitesse. Un premier phénomène concerne le problème avant introduction des PMLs. Une remarque triviale mais très importante est la suivante : en l’absence de perturbation (vitesse constante), il n’y a jamais de réflexion. Autrement dit, pour le problème non perturbé, toute fréquence réelle, et même complexe, est sans réflexion. En revanche, en présence d’une perturbation de la vitesse de type créneau, les fréquences sans réflexion constituent une suite de réels tendant vers l’infini. Ceci est typique de certains problèmes non autoadjoints : une perturbation aussi petite soit elle du cas non perturbé fait passer le spectre du plan complexe tout entier à une suite dénombrable de réels. Ce phénomène étonnant est à l’origine d’un second phénomène qui concerne cette fois la convergence des PMLs lorsque la longueur de troncature L tend vers l’infini. On observe que les valeurs propres calculées dessinent une sorte de fermeture éclair dans le plan complexe, qui s’ouvre lorsque L augmente. Nous montrerons comment cet effet zip peut s’expliquer en introduisant la notion de pseudospectre.

[1] Anne-Sophie Bonnet-Ben Dhia, Lucas Chesnel and Vincent Pagneux, Trapped modes and reflectionless modes as eigenfunctions of the same spectral problem, Proc. R. Soc. A. (2018)

  • Takéo Takahashi, Méthode de la platitude pour la contrôlabilité d’un système d’équations de la chaleur

Nous étudions la contrôlabilité d’un système d’équations de la chaleur en utilisant une approche par « platitude ».
On retrouve en particulier le fait que selon la relation entre les coefficients de diffusion des équations de la chaleur, le système est contrôlable à zéro pour tout T>T_0 , avec T_0\in [0, \infty].
Avec notre méthode, nous obtenons une formule explicite pour le contrôle et pour les solutions correspondantes, et nous montrons que l’état et le contrôle ont une régularité Gevrey en temps et en espace.

  • Philippe Souplet, Singularités des solutions et théorèmes de type Liouville pour l’équation de Hamilton-Jacobi diffusive

Nous considérons l’équation de Hamilton-Jacobi diffusive u_t-\Delta u=|\nabla u|^p, avec conditions de Dirichlet homogènes, qui joue un rôle important en théorie du contrôle stochastique et dans certains modèles de croissance de surface (KPZ).
Malgré sa simplicité, elle présente, dans le cas surquadratique p>2, une variété de comportements intéressants et surprenants. Nous discuterons notamment :

– L’explosion du gradient sur le bord et la forme des singularités ;

– La continuation après l’explosion en une solution globale de viscosité, avec des phénomènes de perte de conditions au bord et de régularisation en des temps multiples ;

– Des théorèmes de type Liouville et leurs applications.

Cet exposé est basé sur une série de travaux en collaboration with A. Attouchi, L. Chabi, R. Filippucci, Y. Li, N. Mizoguchi, A. Porretta, P. Pucci, Q. Zhang.

  • Céline Grandmont, Analyse mathématique et numérique d’un modèle poromécanique linéarisé pour des milieux incompressibles et quasi-incompressibles. Application à la micro-circulation

La plupart des tissus vivants peuvent être modélisés par des systèmes poromécaniques dans lesquels un squelette élastique est perfusé par un fluide.

Dans cet exposé, nous analyserons une version linéarisée du modèle proposé dans [3] et déjà partiellement analysé dans [1], [2]. Une caractéristique de ce modèle est qu’il satisfait à un bilan d’énergie. Après avoir introduit le système couplé, nous montrerons quels sont les arguments principaux de la preuve d’existence de solutions fortes ou faibles dans le cas d’un squelette viscoélastique ou élastique, compressible ou incompressible. Lorsqu’il n’y a pas de dissipation dans le squelette élastique, il s’agit d’un système couplé parabolique-hyperbolique. De plus, dans le cas incompressible, une contrainte de divergence nulle sur la vitesse du mélange apparait. L’étude de la limite incompressible est cruciale dans le cas des tissus vivants qui sont quasi-incompressibles afin de développer des schémas numériques robustes à la limite. Nous présentons et analyserons ensuite des schémas de discrétisation adaptés, dont un schéma de type splitting, complétés par des illustrations numériques. Ce modèle permet en particulier de reproduire des expériences de micro-circulation (perfusion de micro-vaisseaux artificiels). Ces résultats ont été obtenus en collaboration avec Mathieu Barré et Philippe Moireau (INRIA – LMS, Ecole Polytechnique, CNRS – Institut Polytechnique de Paris) dans le cadre de la thèse de Mathieu Barré.

[1] N. Barnafi, P. Zunino, L. Dedè, A. Quarteroni. Mathematical analysis and numerical approximation of a general linearized porohyperelastic model. CAMWA, 2020.
[2] B. Burtschell, P. Moireau, D. Chapelle. Numerical analysis for an energy-stable total discretization of a poromechanics model with inf-sup stability. Acta Mathematicae Applicatae Sinica, English Series, 2019.
[3] D. Chapelle, P. Moireau. General coupling of porous flows and hyperelastic formulations: from thermodynamics principles to energy balance and compatible time schemes. European J. of Mechanics, B/Fluids, 2014.

  • Laurent Thomann, Existence et unicité pour le modèle \Phi^4_3 avec laplacien harmonique

Nous considérons une équation stochastique parabolique non-linéaire avec laplacien harmonique en dimension 3 appelé \Phi^4_3 qui s’écrit

    \begin{equation*} \partial_t X+HX = -X^3 +\infty\cdot X+\xi, \quad t>0, \quad x \in \mathbb{R}^3, \end{equation*}

où H:=-\Delta_{\mathbb{R}^3} +|x|^2 et \xi désigne un bruit blanc spatio-temporel. En utilisant des techniques de calcul para-différentiel développées par Mourrat et Weber pour un problème analogue mais avec des conditions périodiques et des techniques de calcul pseudo-différentiel pour étudier les interactions dues à l’oscillateur harmonique, nous montrons que ce problème (renormalisé) est localement bien posé. Ceci est un travail en collaboration avec Aurélien Deya (Nancy) et Reika Fukuizumi (Tokyo).

Cet exposé concerne l’existence éventuelle de modes piégés dans un milieu de propagation d’ondes occupant un domaine non borné. Un mode piégé est une solution périodique en temps de l’équation des ondes qui présente la particularité d’être auto-existante (au sens où elle ne résulte pas d’une excitation extérieure) et non-rayonnante (ce qui signifie que son énergie est finie et reste confinée dans une région bornée malgré le caractère non borné du domaine de propagation). Du point de vue de la théorie spectrale, l’existence d’un mode piégé revient à la présence d’une valeur propre plongée dans le spectre essentiel de l’opérateur qui régit la dynamique du milieu de propagation.

On s’intéresse au cas des ondes acoustiques modélisées par l’équation de Helmholtz (scalaire). Dans ce cas, il est bien connu que des modes piégés peuvent apparaître dans des guides d’ondes dits « fermés », c’est-à-dire des tuyaux infinis dont la section transverse est bornée. Ceci se produit par exemple en présence d’un renflement local du tuyau ou pour un tuyau coudé : les modes piégés restent alors confinés au voisinage du renflement ou du coude. Que peut-on dire du cas des guides dits ouverts, c’est-à-dire dont la section transverse est non bornée ? L’objet de cet exposé est de présenter quelques résultats récents de travaux communs avec Sarah Al Humaikani, Anne-Sophie Bonnet-Ben-Dhia et Sonia Fliss, réalisés au sein de l’équipe POEMS (CNRS, ENSTA, INRIA).

  • Andreia Chapouto, Théorie des chemins rugueux pour les équations dispersives non-linéaires stochastiques avec des bruits multiplicatifs

Au cours des dernières décennies, le problème de Cauchy pour les équations aux dérivées partielles (EDP) dispersives stochastiques avec des bruits multiplicatifs a fait l’objet de nombreuses études.

Cependant, ces études ont été réalisées principalement du point de vue de la théorie des solutions d’Itô et l’existence de solutions trajectorielles (« pathwise ») reste ouverte.

Dans cet exposé, nous présenterons les premiers résultats du caractère bien-posé « pathwise » pour les équations d’ondes non linéaires stochastiques et les équations de Schrödinger non linéaires stochastiques avec un bruit multiplicatif blanc dans le temps/coloré dans l’espace.

Nous combinons les chemins rugueux contrôlés (« controlled rough path »), adaptés aux flux dispersifs, ainsi que des estimations de tenseurs aléatoires et la « Fourier restriction norm method » (espaces X^{s,b} de Bourgain).

  • Caterina Calgaro, Schémas Volumes Finis pour les équations de Navier-Stokes quantique

Après une introduction aux équations de Navier-Stokes quantiques et un rappel de quelques résultats théoriques, nous présentons deux schémas volumes finis pour résoudre ces équations.
En adaptant le système d’équations, nous développons une méthode numérique capable de capturer les comportements physiques complexes.
L’analyse théorique démontre une décroissance de l’entropie, et confirme la robustesse du schéma proposé.
Les simulations numériques sont en cours de développement, mais les premiers résultats montrent déjà une bonne convergence et stabilité, validant ainsi l’approche proposée.

Cet exposé sera consacré à la description d’un modèle de plasticité parfaite en mécanique des solides permettant d’expliquer l’apparition de déformations permanentes dans un milieu élastique. La présentation se voudra relativement générale et aura essentiellement pour but de décrire le modèle mécanique ainsi que les principaux résultats d’existence mélangeant à la fois des méthodes du calcul des variations et des équations hyperboliques.

  • François Murat, Un problème elliptique singulier unidimensionnel qui présente des résultats inattendus

Dans cet exposé, je présenterai des résultats obtenus en collaboration avec Daniela Giachetti (Rome), Pedro J. Martínez Aparicio (Almería), et Francesco Petitta (Rome), pour le problème aux limites singulier unidimensionnel qui s’écrit formellement

    \[- {{d } \over {d x}} \Big( a (x) {{d u(x)} \over {d x}} \Big) = - {{d g(x)} \over {d x}} - {{d \phi (u (x))} \over {d x}} \;\; {\rm dans} \; (0, L), \quad u(0) = u(L) = 0,\]

où le coefficient a (x) \in L^\infty (0, L) est borné inférieurement par une constante strictement positive et où dans le second membre la fonction g(x) appartient à L^2 (0, L), tandis que le modèle de la fonction non linéaire singulière \phi est donné par {\displaystyle \phi (s) = {{1} \over {| s |^\gamma}} } avec \gamma > 0.

Ce problème singulier présente nombre de phénomènes inattendus : non existence de solutions sous certaines hypothèses, existence d’un nombre infini de solutions sous d’autres hypothèses, et non continuité des solutions par rapport aux approximations des données.

Étant donné un opérateur de Sturm-Liouville en dimension un, dépendant d’un potentiel, la fonction zêta spectrale associée permet de définir son déterminant. On s’intéresse à l’optimisation en fonction du potentiel de cette quantité globale attachée au spectre pour différentes conditions aux limites.

Travail en commun avec Y. Chitour (Paris), P. Freitas (Lisbonne) et Y. Privat (Nancy).

On s’intéresse au contrôle d’une équation de Schrödinger linéaire i\psi'(t)=H(t)\psi(t) où l’état \psi(t) est un point d’un espace de Hilbert complexe (généralement l’espace L^2(M) des fonctions complexes de carrés intégrable sur une variété riemannienne M), et H(t) est un opérateur essentiellement auto-adjoint dépendant du temps, constant par morceaux en temps, et ne pouvant prendre que deux valeurs, H_1 et H_2. On s’intéressera particulièrement au cas où M est le segment [0,1] et H(t) est égal soit au Laplacien Dirichlet, soit au Laplacien Neumann. On montrera comment des techniques de contrôle bilinéaire permettent d’obtenir des résultats de contrôlabilités positifs (et constructifs) ainsi que des résultats négatifs.